什么是分位数？

“分位数（quantile）”一词源于”quantity”。简单地说，分位数就是将样本划分为大小相等、相邻的子组（这就是为什么有时称为 “fractile”）。它也可以指将概率分布划分为具有相等概率的区域。

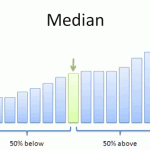
中位数是一种分位数；在概率分布中，中位数被放置在这样一个位置，使得恰好有一半的数据小于中位数，另一半的数据大于中位数。中位数将一个分布切割成两个相等的区域，因此有时也被称为 2-分位数。

https://www.statisticshowto.com/wp-content/uploads/2013/09/median.png

四分位数也是一种分位数；它将分布划分为四个相等的部分。百分位数是将分布划分为 100 个相等部分的分位数，而十分位数是将分布划分为 10 个相等部分的分位数。

有些作者将中位数称为 0.5 分位数，这意味着该比例的值（一半）将位于中位数之下，而另一半则在中位数之上。如果你想在一个数据集中找到特定的分位数（如中位数），使用以下公式来估计第 i 个观测值：

第 i 个观测值 = q * (n + 1)

其中，q 代表你要寻找的第 i 个值以下的比例，n 代表数据集中的项目数量。

上述方程可能有些令人费解，最好通过一个示例来解释。

如何找到分位数？

例题：从以下数据集中找到一个数，使得 20% 的值低于它，80% 的值高于它：
1 3 5 6 9 11 12 13 19 21 22 32 35 36 45 44 55 68 79 80 81 88 90 91 92 100 112 113 114 120 121 132 145 146 149 150 155 180 189 190

思路：

  • 步骤 1：将数据从小到大排序。问题中的数据已经按升序排列。
  • 步骤 2：计算数据集中观测值的数量。这个特定的数据集有 40 个项目。
  • 步骤 3：将任何百分比转换为小数形式的 q。我们要找到其中 20% 的值位于其下方的数字，因此将其转换为 0.2。
  • 步骤 4：将数值代入公式：

第 i 个观测值 = q (n + 1)
第 i 个观测值 = 0.2 (40 + 1) = 8.2

答案：第 i 个观测值为 8.2，所以我们向下取整到 8（记住，这个公式是一个估计）。数据集中的第 8 个数字是 13，它是其中 20% 的值低于它的数字。

参考资料
Quantile: Definition and How to Find Them in Easy Steps：
https://www.statisticshowto.com/quantile-definition-find-easy-steps/

（END）