培养你对数学的直觉

我们对一个新概念的首次接触，往往会形成我们心中对其的第一印象或直觉认知。而这一直觉，也会反过来影响我们在多大程度上喜欢或者认同这个概念。

以“猫”为例，我们可以给出不同角度的定义：

• 山顶洞人视角：一种毛茸茸的动物，具有尖爪、锋利牙齿、灵活尾巴与四条腿，心情愉悦时会发出咕噜声，生气时会发出威胁的嘶嘶声……
• 进化论视角：作为猫科动物的一员，猫是哺乳类动物的一个物种，拥有某些共同遗传特征……
• 现代基因视角：猫不过是拥有以下DNA序列的动物：ACATACATACATACAT……

(插图来源：Common Craft）

毫无疑问，现代基因视角提供了最准确的定义。但是，这就足以成为解释“猫”的最佳起点吗？如果要让一个孩子理解“猫”的含义，我们会只给出这种定义吗？它能让我们深入理解猫的本质吗？答案似乎是否定的。现代定义固然准确实用，但应建立在对“猫”有一定认识的基础上，而非概念学习的起点。

不幸的是，数学理解往往也遵循类似的模式。我们被教授现代严谨的定义，而不是产生这些定义的逻辑过程。我们只掌握了晦涩难懂的公式，而对其背后的数学思想知之甚少。

我们不妨换个角度思考。想象一个圆圈：中心是你正在学习的概念，圆周上是描述该概念的事实。我们可以从一个小的切入点开始，一个事实或见解，然后逐步拓展我们的思路。从“猫有共同的身体特征”引出“猫有共同的祖先”，再引出“一个物种可以通过 DNA 某些部分来识别”。 这样我们可以看到，现代基因定义是从早期定义逐步推导出来的。

但并不是所有的起点都一样。正确的视角能让数学更容易理解——最先发现这些概念的“数学原人”往往拥有启发性的视角。

现在，我们来看一个数学例子，讨论一下圆的定义。并从中学习如何建立直觉，重拾数学的原初逻辑。

什么是“圆”？

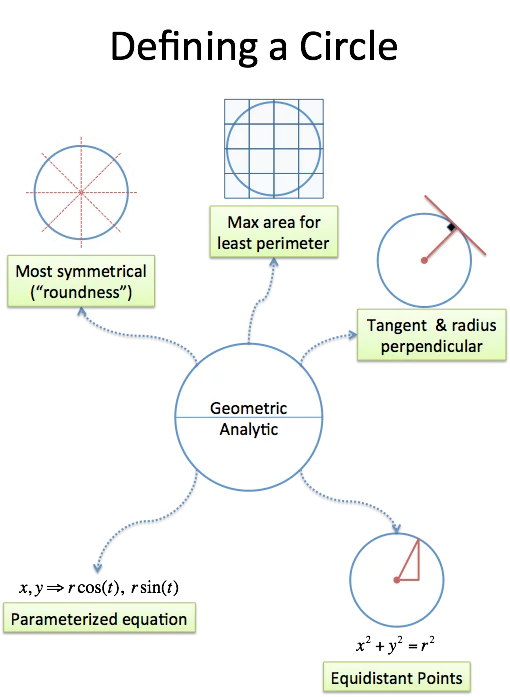
圆有许多不同的定义，以下是其中一些：

• 圆是最对称的二维平面图形。
• 在相同周长的情况下，面积最大的图形就是圆。
• 圆是平面上与给定点距离相等的所有点的集合（用圆规或铅笔在绳子上画出的点）。
• 圆是满足公式 x²+y²=r²（其中 r 为大于 0 的已知实数）的所有点（x,y）的集合。（上述几何定义的解析版本）。
• 圆是满足方程 x=rsin(t) 和 y=rcos(t)（其中 r 为大于 0的已知实数，t 为任意实数）的所有点（x,y）的集合（这是真正的解析版本）。
• 任意一条切线都垂直于“切点的位置向量”的图像就是圆（这是物理解释）。

这样的定义举不胜举，但它们都描述的是同一个概念！就像说 1、one、uno、eins、“2x + 3 = 5 的解”或“你脸上鼻子的数量”，它们只是用不同的名称来表达同一个概念。

然而，这些最初的描述非常重要，因为它们塑造了我们的直觉。因为在我们上课之前，在现实世界中我们就看到过圆，所以我们知道什么是圆。无论我们看到多么复杂的等式（如 x² + y² = r²），我们内心深处都知道圆是“圆”的。如果我们将这个等式画成图形，但它看起来是方的或者是扁的，我们也可以知道这是错误的。

在我们孩提时代，我们学习了“山顶洞人”对圆的定义（一个真正的圆形物体），这给了我们一种舒适的直觉。我们能够看到，在圆上的每一个点到圆心的距离都是相等的。而表达这个事实的解析式就是 x² + y² = r²，它利用了勾股定理来表示距离。我们从这种直觉出发，逐步演绎出了正式的定义。

然而，对于其他概念来说，情况可能没有圆那么幸运。我们是否本能地理解自然常数 e 的增长，或者它只是一个抽象的定义？我们是否意识到虚数单位 i 的旋转，或者它只是一个人为的、无用的概念？

培养洞察力的策略

我仍然不得不时刻提醒自己去理解 e 和 i 的深层含义，这看起来似乎很荒谬，就像要“记住”圆是什么形状，猫是什么样子一样。这本应该是我们与生俱来的直观认知。

缺乏全局观让我感到沮丧：数学的本质是思想，公式只是表达思想的一种方式。一旦中心概念明确了，相关的方程式也就迎刃而解。以下是一个对我很有帮助的策略：

步骤 1：找到数学概念的中心主题。尝试从历史的角度入手。这个概念最早是在哪里使用的？它的发现者当时在追求什么目标？这种早期使用可能与我们现代的解释和应用有所不同。

步骤 2：利用主题来解释一个属性或事实。将其与正式定义进行类比。如果幸运的话，你可以将数学公式（如x² + y² = r²）转化为通俗易懂的语言陈述（“所有点到中心的距离相同”）。

步骤 3：利用相同的主题来探索其他相关属性。一旦你找到一个有效的类比或解释，看看它是否适用于其他属性。有时候，这个类比是有用的，有时候可能不够适用（这时你需要寻找新的见解），但你会惊喜地发现许多意想不到的发现。

我们来试试看。

一个真实的例子： 理解自然常数 e

自然常数 e 出现在科学的各个领域，有许多定义，但很少能以一种自然的方式被理解。让我们围绕这个概念展开深入探讨。下文将列出几个等式，这些等式都是一些简单的描述概念的方法。即使等式本身可能听起来不可思议，它们背后也有一个浅显易懂的概念。

以下是几个流行的 e 的定义：

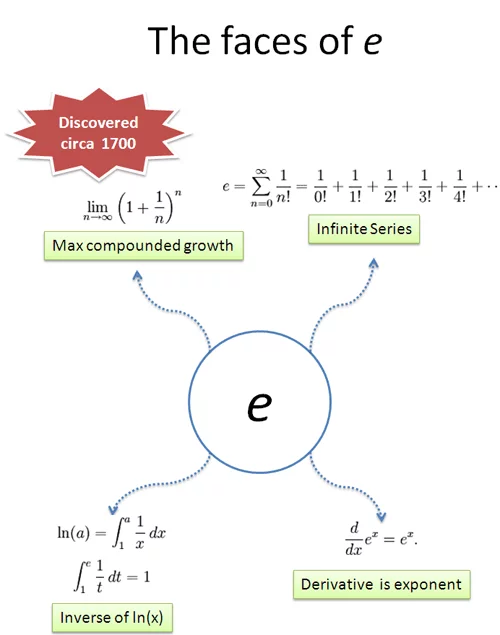
首先要做的是确定一个主题。从 e 的历史来看，它似乎与增长或利率有关。实际上，e 的发现并非来自抽象的数学猜想，而是在商业计算中被应用，因此“利息”（增长）可能是一个相关的主题。

现在，让我们来看看左上角的第一个定义。对我来说，关键的一步是意识到这个等式看起来非常像复利的计算公式。事实上，它就是复利计算公式，即在一个单位的时间内，以最快的速度复合计算 100% 的利息。

定义 1：将 e 定义为以最小增量实现 100% 的复利复合增长。

接下来，我们看看第二个定义：一个趋向于零的无限项级数。这代表什么呢？

在以“利息”为主题进行思考之后，我们发现这个定义展示了复利的组成部分。然而，获得这样的洞察力并不是一蹴而就的，这种洞察力可能是在头脑风暴中想象“当讨论增长时，1 + 1 + 1/2 + 1/6 + …… ”代表着什么。

让我们逐项解释这个序列。第一项（1 = 1/0!，记住 0 的阶乘等于 1）代表的是你的本金，即原始金额。下一个项（1 = 1/1!）是你赚取的“直接”利息——相当于本金的 100%。再下一个项（0.5 = 1/2!）是你赚取的“第二级利息”的金额。再下一个项（0.1666 = 1/3!）是你的“第三级利息”——也就是你的利息所赚取的金额。

这个序列展示了钱生钱的过程，每个阶段都有对应的贡献，将这些贡献逐步分开。还有很多其他方面可以探讨，但这就是以“增长”为核心来理解这个概念的要点。

因此，第二个定义可以表述为： 根据每个利息增长对总的资金的贡献来定义 e。

现在来看看第三个，也是最简短的定义。它到底意味着什么呢？不要陷入计算方程式的思维模式，不要去想“导数”，试着理解等式的感觉，让它成为你的朋友。

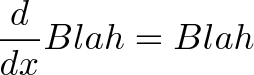
这个定义告诉我们，按照微积分的说法，“你的增长率等于你当前的金额”。那么，以当前金额增长就是 100% 的利率，对吗？持续增长意味着不断计算利息——这是另一种连续复利的描述方式！

因此，第三个定义可以表述为：将 e 定义为始终以当前值的 100% 增长的函数。

没错，e 是一个数字，在这个数字上，你总是以当前金额（100%）增长，而不是 1% 或者 200%。

现在来到了最后一个定义的时间——这是一个棘手的问题。我这样来解释它：与其描述你成长了多少，为什么不说你花了多长时间呢？

假设你的速度是 1，并且以 100% 的速率增长，那么从 1 增长到 2 需要一个单位的时间！从 3 增长到 4 只需要 1/3 个单位的时间，以此类推。

从 1 增长到 A 所需的时间就是从 1 到 2，从 2 到 3，从 3 到 4……一直持续下去，直到达到 A。

简单地说，ln(a) 表示从 1 增长到 a 所需的时间。我们可以说，e 是刚好需要 1 个单位的时间才能增长到的数字。换句话说，e 就是在等待 1 个单位时间后的增长量！

因此，第四个定义可以表述为：将从 1 持续增长到 a 所需的时间定义为 ln(a)。

怎么样？一旦我们掌握了核心理念（“e 是 100% 的连续增长”），那些复杂的方程式就能够轻易推导出来——微积分可以被用英语来表述。数学是关于思想的！

寓意何在？

在数学课上，我们常常从最后一个最复杂晦涩的概念开始讲解。这也难怪我们会感到困惑——我们拿着 DNA 的示意图，却期望学生看到一只猫。

我从这种方法中学到了一些经验，它是我理解和解释数学的基础：

• 寻找洞察力并加以应用。第一个直观的洞察力可以帮助其他所有的事情都水到渠成。从一个有意义的定义开始，“绕着圈子走”，找到其他的定义。
• 培养心理韧性。用你大脑和一个新概念较劲并不好玩。如果不理解，可以换个角度思考。其他书籍、文章、人的解释可能对你更有意义。
• 视觉化也是行之有效的方法。虽然我们通常认为数学是死板的、分析性的，但是通过视觉解释也能够深入理解。尝试进行能够加深理解的实践活动。就拿虚数来说，几十年后人们才发现它与几何的关联。整天盯着方程式看并不能帮助数学家真正 “理解” 其含义。

当我们过分强调定义而忽略理解时，数学就会变得困难。要记住，现代的定义只是最先进的思维步骤，但并不一定是起点。不要害怕从一个有趣的角度去理解一个概念，试着找出那些能用通俗易懂的句子来描述等式背后含义的方法。

原文链接：https://betterexplained.com/articles/developing-your-intuition-for-math/

（END）