如无特别说明，本文源码基于 JDK 1.8 进行解读。

从 HashMap 的源码中的 get(Object key) 和 put(K key, V value) 两个基本操作方法中，我们可以发现，要从一个 HashMap 中获取某个 key 对应的哈希桶位置，需要先通过 hash(Object key) 方法计算出 hash 值，再通过位运算 (n - 1) & hash 得出哈希桶位置。

相关源码如下（这里以 get(Object key) 方法为入口）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 获取 key 的哈希值
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

// 获取 key 对应的值
public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

// 获取 key 对应的值，具体获取逻辑
final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        if ((e = first.next) != null) {
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    return null;
}

我们可以把 HashMap 的哈希函数归结为以下两个步骤：

  • 计算 key 的哈希值 hash；
  • 将哈希桶数量 n 减去 1，再与哈希值 hash 做按位与运算。

具体的哈希逻辑如下图：

哈希逻辑

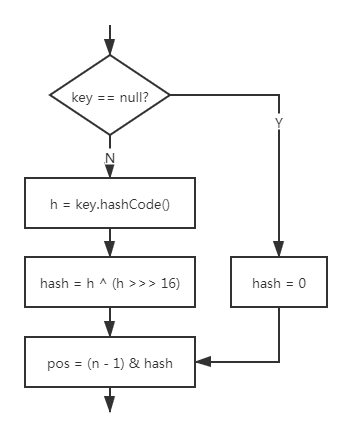
其中， h 为 key 的哈希码（通过 hashCode() 获取），hash 为 key 的哈希值，pos 为哈希桶位置（哈希数组下标）。

整个逻辑比较简单，也符合哈希函数的简单高效的特性。不过，你可能会对其中两个位运算的步骤感到疑惑：

  • 第一，为什么 hash 要取 h ^ (h >>> 16)，直接取 h 不行吗？
  • 第二，为什么获取哈希桶位置是 (n - 1) & hash，而不是常用的取模运算 hash % n？

接下来，我们就聊聊这两个问题。作为一个常用的映射类，为了尽可能提升 HashMap 的性能，JDK 的开发者都做了哪些巧妙的设计和优化。

我们先来看看第二个问题，因为知道了 (n - 1) & hash 是怎么设计的，就会很容易理解 hash 值不直接使用 h，而是用 h ^ (h >>> 16) 的原因。

为什么获取哈希桶位置是 (n - 1) & hash？

这里的 n 代表哈希表的长度（或称哈希桶数量，对应 HashMap 数组结构的大小），其大小被设计为 2 的幂，如

这么设计是因为恰好可以保证 (n - 1) & hash 的运算结果的范围总是在 [0, n-1] 内，即总是在 HashMap 数组的下标之内。

例如：

当 hash = 7，n = 16 时，(n - 1) & hash = 7；

当 hash = 19，n = 16 时，(n - 1) & hash = 3；

当 hash = -9，n = 16 时，(n - 1) & hash = 7。

可运行以下代码进行校验：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class HashMapTmpApp {
    public static void main(String[] args) {
        // 哈希表长度
        int n = 16;
        // hashCode数组
        int[] hashCodes = {7, 19, -9};

        for (int hash : hashCodes) {
            System.out.printf("(%d - 1) & %d = %d \r\n", n, hash, (n - 1) & hash);
            System.out.println(hash % 16);
        }
    }

    /*
    此代码示例执行结果如下：
    (16 - 1) & 7 = 7
    (16 - 1) & 19 = 3
    (16 - 1) & -9 = 7
     */
}

那为什么哈希表的长度被设计为 2 的幂时，(n - 1) & hash 的结果恰好可以保证在哈希数组范围 [0, n-1] 内呢？

在回答这个问题之前，我们先来看看按位与运算的规则：

当对应的两个二进位数都为 1 时，相应的结果位才为 1，否则为 0。

其实这里还有一个相对比较“隐蔽的规律或者现象”：当两个二进制数进行按位与运算时，如果其中一个二进制数的某一个位为 1，则按位与运算的结果的相应位上是保留了另一个二进制数在该位上的数。

有点绕口，我们举例来说明。

假设存在两个二进制数 A 和 B， 其中，A = 1100，第三、四位都为 1，

当 B = 0110 时，A & B = 0100，运算结果的第三位为 1，第四位为 0，即保留了二进制数 B 的第三、四位上的数；

当 B = 1001 时，A & B = 1000，运算结果的第三位为 0、第四位为 1，即保留了二进制数 B 的第三、四位上的数；

理解了按位与运算的这一规律之后，我们再来看 n 和 n - 1 的二进制表示的规律。

我们知道，哈希表的长度 n 被设计为 2 的幂，我们记为

当 m = 1 时，n = 2，n - 1 = 1，其对应的二进制如下表：

十进制 二进制
n 2 0000 0000 0000 0000 0000 0000 0000 0010
n - 1 1 0000 0000 0000 0000 0000 0000 0000 0001

当 m = 2 时，n = 4, n - 1 = 3，其对应的二进制如下表：

十进制 二进制
n 4 0000 0000 0000 0000 0000 0000 0000 0100
n - 1 3 0000 0000 0000 0000 0000 0000 0000 0011

当 m = 3 时，n = 8, n - 1 = 7，其对应的二进制如下表：

十进制 二进制
n 8 0000 0000 0000 0000 0000 0000 0000 1000
n - 1 7 0000 0000 0000 0000 0000 0000 0000 0111

当 m = 4 时，n = 16, n - 1 = 15，其对应的二进制如下表：

十进制 二进制
n 16 0000 0000 0000 0000 0000 0000 0001 0000
n - 1 15 0000 0000 0000 0000 0000 0000 0000 1111

可以发现，$n=2^m$ 的二进制形式为 1 后面跟着 m 个 0，$n-1=2^m-1$ 的二进制形式为后面有 m 个 1。

结合以上的按位与运算规律和二进制数规律，可以得出这个结论，无论 hash 的值是多少，将其转成二进制，跟 n - 1 的二进制进行按位与运算，得到二进制结果，前 (32 - m) 位都为 0，后 m 位为 hash 的二进制数的后 m 位。这也就是说二进制的结果大小被限制在后 m 位，对应十进制大小范围就是 $0$ 到 $2^m-1$。

例如，假设哈希表长度 n = 16，即 $n=2^4$，那么 $n - 1 = 15$，其对应的二进制为：

0000 0000 0000 0000 0000 0000 0000 1111。

将其与 hash 的二进制数进行按位与运算，得到二进制结果，前 28 位都为 0，后 4 位为 hash 二进制数的后 4 位，相当于保留 hash 的二进制数后 4 位。

所以，

0000 0000 0000 0000 0000 0000 0000 1111 & hash

的结果一定是在

0000 0000 0000 0000 0000 0000 0000 0000

到

0000 0000 0000 0000 0000 0000 0000 1111

之间，对应的十进制范围就是 [0, 15]。

到这里，应该能理解通过位运算 (n - 1) & hash 得到的结果，最终也能正确映射到哈希桶的位置。

我们知道，位运算是计算机底层的操作，运行速度要比模运算快。而且，如果使用 hash % n 来计算哈希桶位置，还要考虑 hash 小于 0 的情况。在追求极致性能上，多一个小小的判断无疑都会造成性能的损耗。这就是为什么获取哈希桶位置是 (n - 1) & hash，而不是 hash % n 的原因。

简而言之，就是通过位运算来提升哈希表性能。

理解了第二个问题，现在我们回过头来看第一个问题。

为什么 hash 要取 h ^ (h >>> 16)？

通过上面的分析知道，(n - 1) & hash 的运算结果就是保留了 hash 的二进制数后 m 位，其中，$n = 2^m$。

这意味着，只要 hash 值的二进制数后 m 位是一样的，那么最终计算出来的哈希桶位置 pos 肯定都是一样的（我们把这称为哈希冲突）。

例如，当 m = 4 时，n = 16，以下 hash 值，它们的二进制数后 4 位相同，都为 1011，那么通过 (n - 1) & hash 计算出的哈希桶位置都是一样的。

0000 0100 0000 0000 0000 0000 1000 1011，
0000 0110 0000 0000 0000 0000 0100 1011，
0000 0001 0000 0000 0000 1111 0100 1011，
0011 0010 0000 0000 0000 1000 0000 1011。

计算过程如下：

(n - 1) & hash = 15 & hash

转为二进制：

0000 0000 0000 0000 0000 0000 0000 1111 & hash

将上例 hash 值的二进制数代入，最终计算出的结果为：

0000 0000 0000 0000 0000 0000 0000 1011。

为了降低这种哈希冲突的概率，JDK 的开发者通过合并 h 的高位和低位来增加随机性。具体的操作就是将 h 无符号右移 16 位，并将 h 与右移后的结果进行了异或运算。

如将二进制数 h = 0000 0100 0100 0001 0000 0000 1000 1011 无符号右移 16 位，结果为：

h >>> 16 = 0000 0000 0000 0000 0000 0100 0100 0001

通过异或运算合并 h 的高位和低位：

h ^ (h >>> 16) =
0000 0100 0100 0001 0000 0000 1000 1011 ^
0000 0000 0000 0000 0000 0100 0100 0001 =
0000 0100 0100 0001 0000 0100 1100 1010

最后再通过按位与运算计算出哈希桶位置：

(n - 1) & hash =
0000 0000 0000 0000 0000 0000 0000 1111 &
0000 0100 0100 0001 0000 0100 1100 1010 =
0000 0000 0000 0000 0000 0000 0000 1010

也就是说，虽然 h 的后 4 位 1011 跟上面例子中的二进制后 4 位相同，但经过合并高位和低位，最终计算出的哈希桶位置是不同的。这在一定程度上降低了哈希冲突的概率。

不过，这仅仅是一种在速度、实用性和位运算质量方面的一种折衷方式。因为即使不通过合并高位和低位的方式处理，许多常见的哈希值本来也能合理均匀分布，所以也就不会从这种方式中受益。并且，在实际使用中，当存在大量哈希冲突时，HashMap 还会把链表进行树化，即转化为红黑树进行处理。所以，通过右移和异或运算，是在尽可能少影响原本性能的基础上，通过合并高位和低位来增加随机性。否则，高位上的数可能永远不会参与到哈希桶位置的计算中。

简而言之，就是通过合并 key 的 hashCode 值的高位和低位，以此来加大随机性，从而在一定程度上降低哈希冲突概率。

小结

本文通过源码分析了 HashMap 的哈希函数，并着重分析了函数中的所使用到位运算。把 key 的 hashCode 值从高位移到低位，并使用异或运算，目的是降低哈希冲突概率。使用按位与运算代替取模运算，则是为了提高性能。